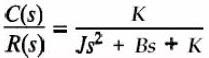ANÁLISIS DE RESPUESTA TRANSITORIA

SISTEMAS DE SEGUNDO ORDEN

Respuesta escalón de sistemas de segundo orden. La función de transferencia en lazo cerrado del sistema:

Los polos en lazo cerrado son complejos si B²-4JK<0 y son reales si B²-4JK>0. En el análisis de la respuesta transitoria, es conveniente escribir:

en donde σ se denomina atenuación; ωn frecuencia natural no amortiguada y ξ factor de amortiguamiento relativo del sistema. El factor de amortiguamiento relativo ξ es el cociente entre amortiguamiento real B y el amortiguamiento crítico Bc=2√JK, o bien:

entonces en términos de ξ y ωn:

Determinando polos:

S²+2ξωn+ωn²= 0

donde los polos pueden ser:

Reales: ξ>1 (SISTEMA AMORTIGUADO)

Reales e iguales: ξ=1 (SISTEMA CRITICAMENTE AMORTIGUADO)

Complejos conjugados: 0<ξ<1 (SISTEA SUB-AMORTIGUADO)

Definiciones de las especificaciones de respuesta transitoria:

Con frecuencia, las características de desempeño de un sistema de control se especifican en términos de la respuesta transitoria para una entrada escalón unitario, dado que ésta es fácil de generar y es suficientemente drástica. (Si se conoce la respuesta a una entrada escalón, es matemáticamente posible calcular la respuesta para cualquier entrada.)
La respuesta transitoria de un sistema para una entrada escalón unitario depende de las condiciones iniciales. Por conveniencia al comparar respuestas transitorias de varios sistemas, es una práctica común usar la condición inicial estándar de que el sistema está en reposo al inicio, por lo cual la salida y todas las derivadas con respecto al tiempo son cero. De este modo, las características de respuesta se comparan con facilidad.
La respuesta transitoria de un sistema de control práctico exhibe con frecuencia oscilaciones amortiguadas antes de alcanzar el estado estable. Al especificar las características de la respuesta transitoria de un sistema de control para una entrada escalón unitario, es común especificar lo siguiente:

1. Tiempo de retardo, td
2. Tiempo de levantamiento, tr
3. Tiempo pico, tp
4. Sobrepaso máximo, Mp
5. Tiempo de asentamiento, ts

1. Tiempo de retardo, td: el tiempo de retardo es el tiempo requerido para que la respuesta alcance la primera vez la mitad del valor final.
2 . Tiempo de levantamiento, tr: el tiempo de levantamiento es el tiempo requerido para que la respuesta pase del 10 al 90%, del 5 al 95% o del 0 al 100% de su valor final. Para sistemas subamortiguados de segundo orden, por lo común se usa el tiempo de levantamiento de 0 a 100%.
Para sistemas sobreamortiguados, suele usarse el tiempo de levantamiento de 10 a 90%.
3. Tiempo pico, tp: el tiempo pico es el tiempo requerido para que la respuesta alcance el primer pico del sobrepaso.
4 . Sobrepaso máximo (porcentaje), Mp el sobrepaso máximo es el valor pico máximo de la curva de respuesta, medido a partir de la unidad. Si el valor final en estado estable de la respuesta es diferente de la unidad, es común usar el porcentaje de sobrepaso máximo. Se define mediante:

porcentaje de sobrepaso máximo =

La cantidad de sobrepaso máximo (en porcentaje) indica de manera directa la estabilidad
relativa del sistema.

5. Tiempo de asentamiento, ts: el tiempo de asentamiento es el tiempo que se requiere para que la curva de respuesta alcance un rango alrededor del valor final del tamaño especificado por el porcentaje absoluto del valor final (por lo general, de 2 a 5%) y permanezca dentro de él. El tiempo de asentamiento se relaciona con la mayor constante de tiempo del sistema de control. Los objetivos del diseño del sistema en cuestión determinan cuál criterio de error en porcentaje usar.

Especificaciones de la respuesta transitoria:

Excepto para ciertas aplicaciones en las que no se pueden tolerar oscilaciones, es conveniente que la respuesta transitoria sea suficientemente rápida y amortiguada. Por tanto, para una respuesta transitoria conveniente de un sistema de segundo orden, el factor de amortiguamiento relativo debe estar entre 0.4 y 0.8. Valores pequeños de ξ(ξ<0.4) producen un valor de sobrepaso excesivo en la respuesta transitoria, y un sistema con un valor grande de

ξ(ξ>0.8) responden con lentitud.

Sistemas de segundo orden y especificaciones de la respuesta transitoria.

A continuación, obtendremos el tiempo de levantamiento, el tiempo pico, el sobrepaso máximo y el tiempo de asentamiento del sistema de segundo orden Estos valores se obtendrán en términos de ξ; y ωn. Se supone que el sistema está subamortiguado.

Tiempo de levantamiento:

Tiempo pico:

Sobrepaso máximo:

Tiempo de asentamiento:

(criterio del 2%)

(criterio del 5%)

PROCEDIMENTO PRÁCTICO:

Esquema del sistema Eléctrico RLC:

R=137 Ω
L=10 mH
C=0.1 uF

Ecuaciones Matemáticas:

Aplicando Laplace:

La función de transferencia es:

Aplicado en MATLAB:

» R=137;
» L=0.01;
» C=0.000001;
» num=[1];
» den=[L.*C R.*C 1];
» g1=tf(num,den)

Transfer function:
1
---------------------------
1e-008 s^2 + 0.000137 s + 1

» step(num,den)

Circuito Realimentado:

» feedback(g1,1)

Transfer function:
1
---------------------------
1e-008 s^2 + 0.000137 s + 2

» m=feedback(g1,1)

Transfer function:
1
---------------------------
1e-008 s^2 + 0.000137 s + 2

» step(m)

Resultados:

MULTISIM:

CIRCUITO REALIMENTADO

Cálculos de circuito realimentado (usando 2 OPAM):

Luego en el siguiente esquema hacemos variar el potenciómetro tenemos:

Para 2 KΩ:

Para 5 KΩ:

Para 0.5 KΩ:

CONCLUSIONES

- La respuesta en el tiempo de un sistema de control consta de dos partes: la respuesta transitoria y la respuesta en estado estable.

- En laboratorio desarrollado, pudimos observar el comportamiento del sistema de segundo orden a través del osciloscopio y todos parámetros correspondientes.

- En el circuito realizado nos percatamos que el uso del OPAM en un circuito retroalimentado hace que su implementación sea más práctica y sencilla.

- En la práctica es importante conocer el tiempo de establecimiento para que nuestro sistema retroalimentado sea óptimo en todo sistema de control.